Elliptic curve basics

Singular points

Let’s have an elliptic curve:

$E: y^2 = x^3 + a x + b$

Let’s define:

$F(x, y) = y^2 - x^3 - a x - b$

The singular points are the points on the curve where both partial derivatives of $f$ vanish:

$\frac{\partial F}{\partial x} = \frac{\partial F}{\partial x} = 0$

Let’s observe the following two elliptic curves:

$E_1: y^3 = x^3 + x$

$E_2: y^3 = x^3 + x^2$

The corresponding images would be (all images by Desmos (opens new window))

and

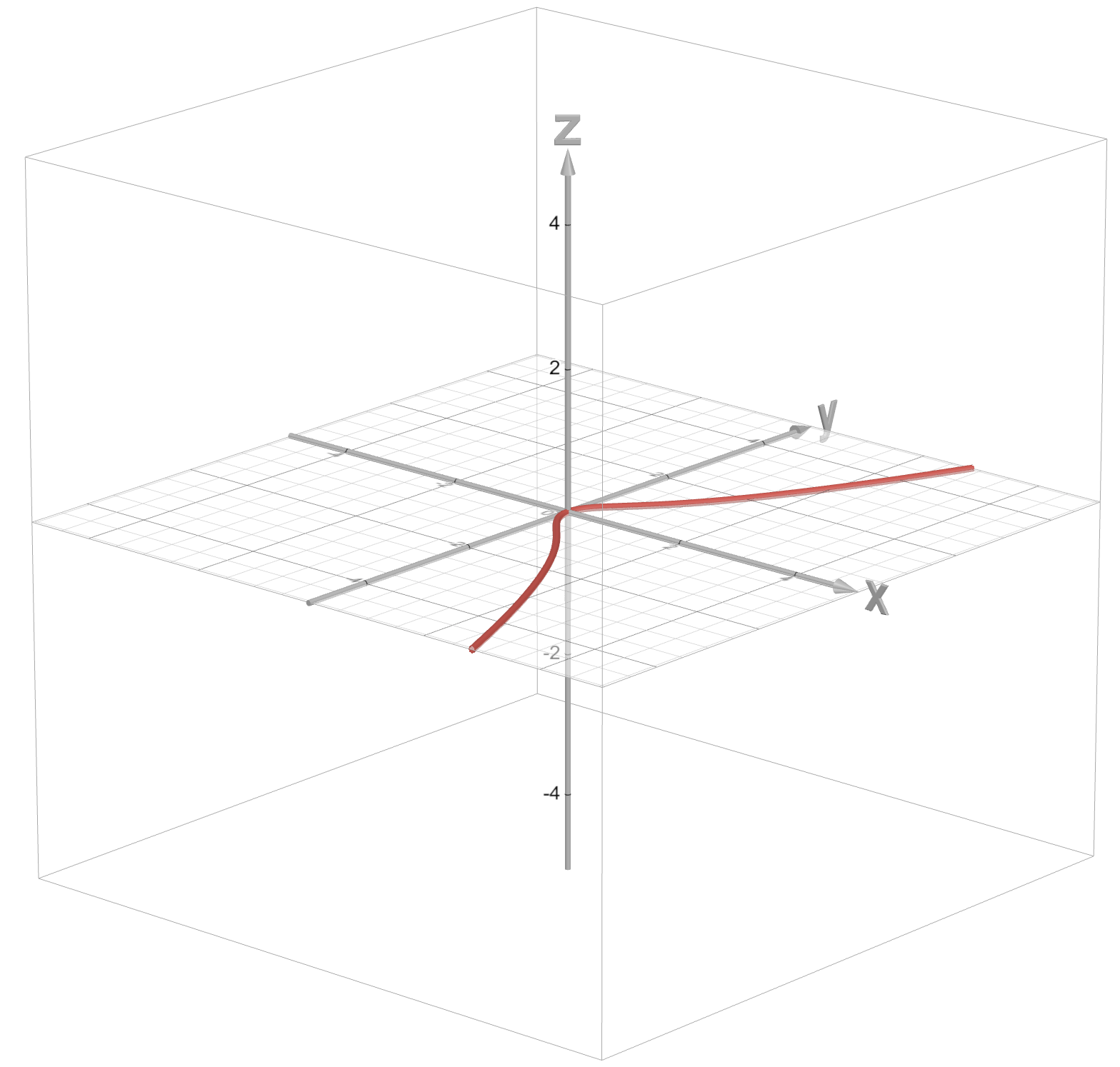
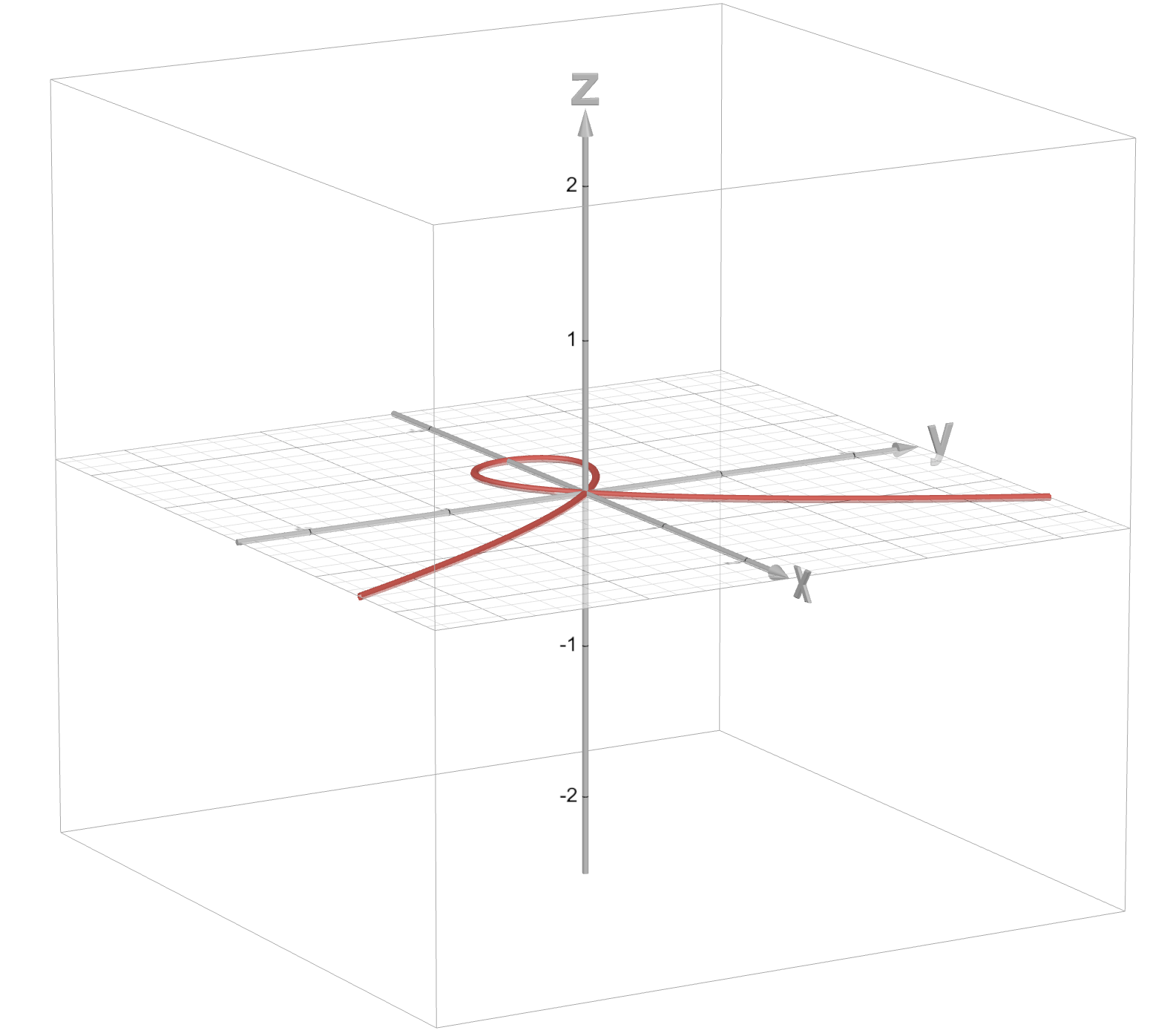
And the corresponding functions would be:

$F_1: y^3 - x^3 - x$

and

$F_1: y^3 - x^3 - x^2$

For $E_2$ at point $(0, 0)$ we get: $\frac{\partial F}{\partial x} = \frac{\partial F}{\partial x} = 0$. So this is a singular point.

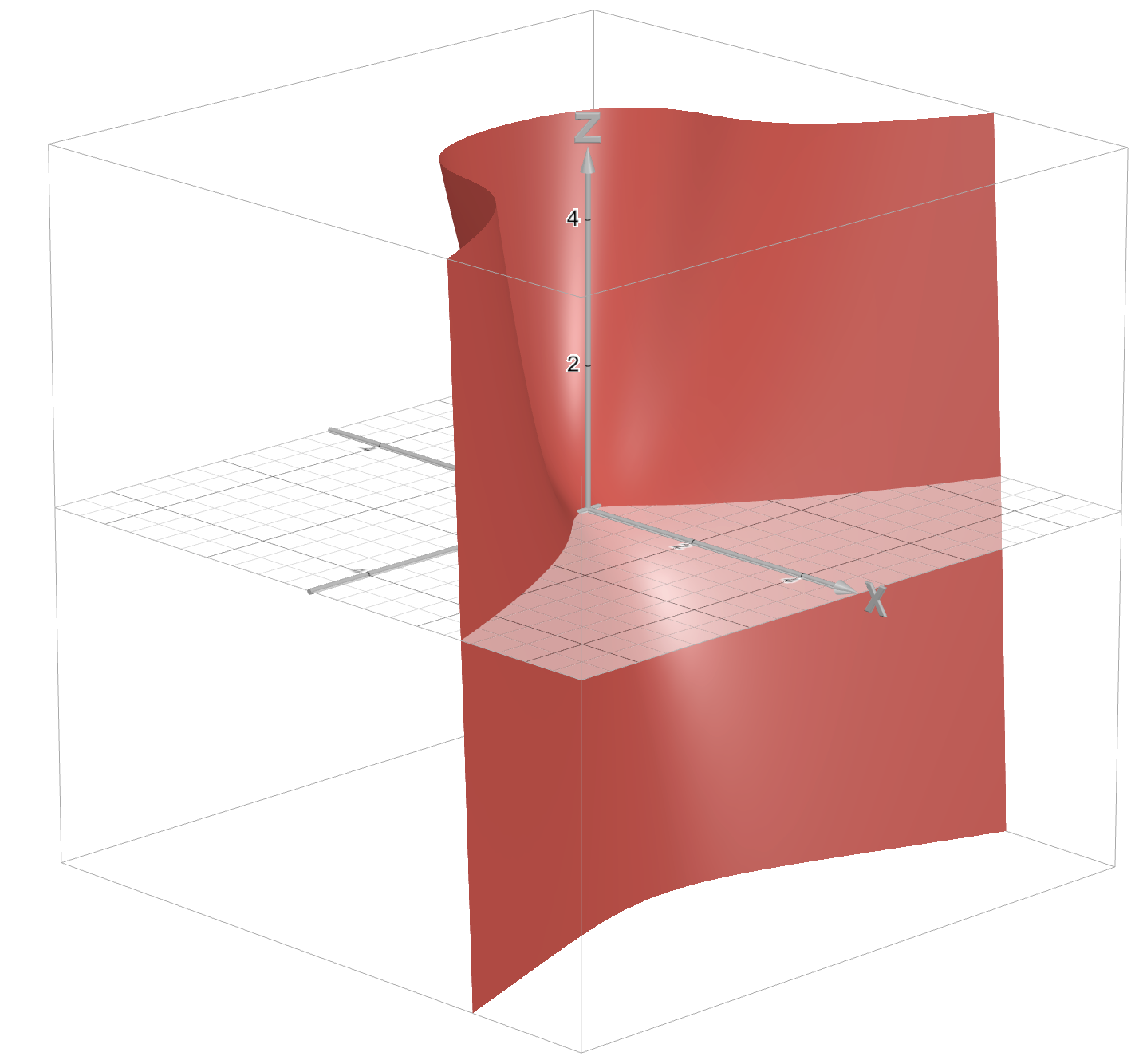
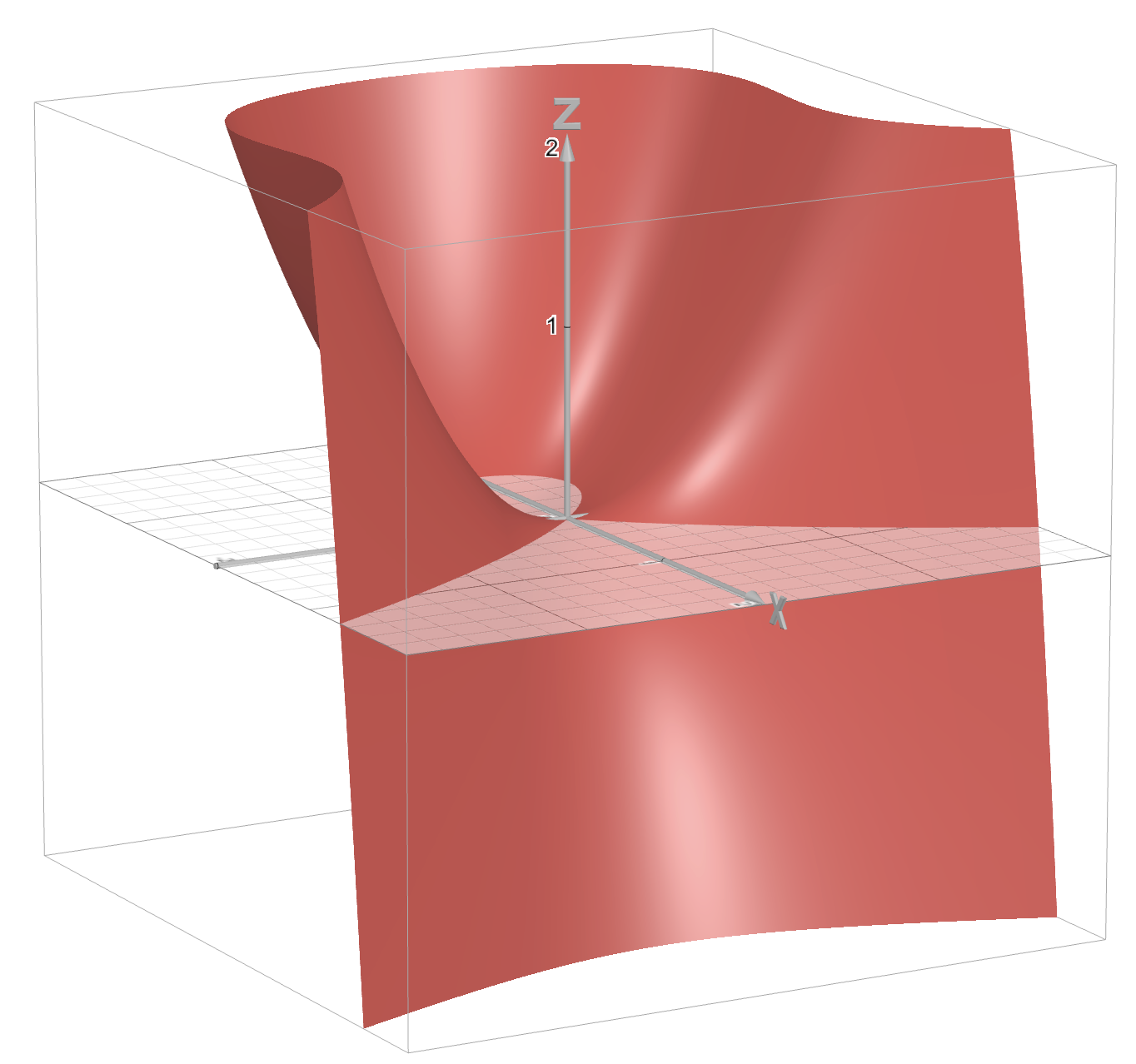
I wanted to at least intuitively understand why the singular points are problematic. We have $\frac{\partial F_2}{\partial x} = 0$ at $(0, 0)$. If we fix $y = 0$ and observe how $F$ changes when $x$ changes, we see that $F_2$ has a local extremum at $x = 0$.

Similarly, observing that $\frac{\partial F_2}{\partial y} = 0$, we see that $F_2$ has a local extremum at $y = 0$. However, when we move along the $x$-axis, we are below $0$, and when we move along the $y-$axis we are above $0$. So, it’s clear that these cases are special.

Points of order 2

Is there something special about the points of order $2$?

Yes, the point of order $2$ are the points that have a vertical tangent. Why is this so?

Let’s have an elliptic curve in short Weierstrass form (both curves mentioned above are in this form):

$E: y^2 = x^3 + a x + b$

Note that when we have a field of characteric greater than $3$, we can transform the generalized Weierstrass form

$E: y^2 + a_1 x y + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6$

into a short form.

In short Weierstrass form, if $(x, y) \in E$, then $(x, -y) \in E$.

From the definition of the operation on the elliptic curve, it holds:

$-(x, y) = (x, -y)$

So we see that the points of form $P = (x, 0)$ are special—their negation is the same point:

$P = -P$

$2P = 0$

Thus, points of the form $P = (x, 0)$ are the ones that have order $2$. But why is there a vertical tangent?

I am sure there are better way to see it, but I looked at it this way: let’s consider a point $P = (x, 0)$ of order $2$. For any $R \in E,$ $R + R$ is defined by taking the tangent at $R$ and finding the intersection of the tangent with $E$. So, if we take the tangent at $P = (x, 0)$ of order $2$, and if the tangent is not vertical, it will intersect some point $Q \in E$. This would mean that

$2P = Q \neq 0$

which would contradict the order of the point $P$.

Why is there no intersection of the vertical tangent at a point of order $2$ with an elliptic curve $E$?

Let’s observe the image below. We have $E: y^2 = x^3 + a x + b$. Let’s fix $x = 2$ (since in the example on the image $P = (2, 0)$) and observe

$y^2 - x^3 - a x - b$

as a function of $y$ at $x = 2$ (one would need to rotate their head for 90 degrees when observing the image), the derivative is $2 y$. This derivative only has one zero, so there is only one local extremum, Therefore, the image is clearly incorrect as there are two local extremums.

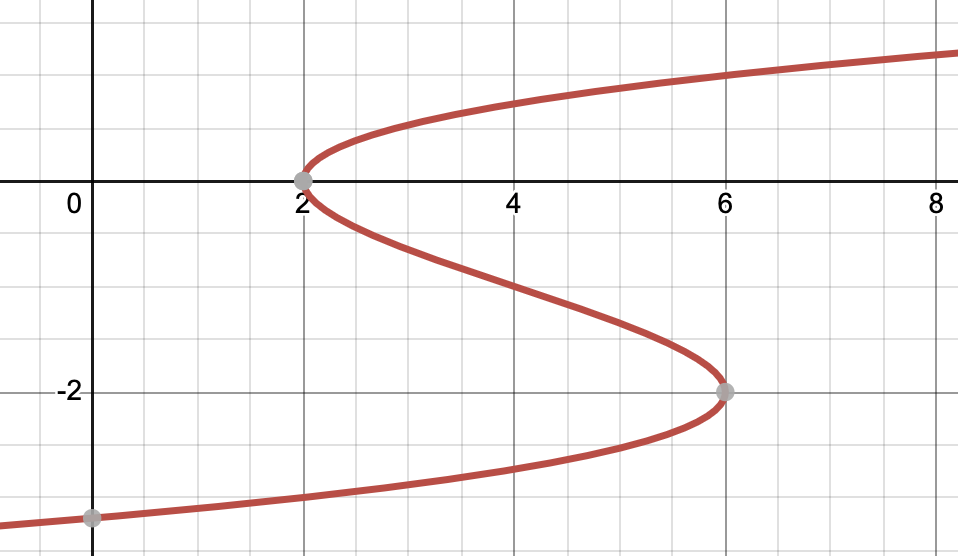
How do we find the points of order $2?$ We need to find the roots of the equation $x^3 - a x - b.$

Note that that the points of order at most $2$ (which includes the point at infinity $0$) form either the Klein-4 group or a cyclic group of order $2$, depending on whether all roots are real or not. However, I won’t go into it now.

General Weierstrass form

Negate the point

Let’s consider an elliptic curve in the generalized Weierstrass form:

$E: y^2 + a_1 x y + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6$

If we have $P = (x, y) \in E$, then

$-P = (x, -y - a_1 x - a_3)$

We can see this from observing:

$y(y + a_1 x + a_3) = x^3 + a_2 x^2 + a_4 x + a_6$

If we replace $y$ with $-y - a_1 x - a_3$ we obtain

$(-y - a_1 x - a_3) (-y) = x^3 + a_2 x^2 + a_4 x + a_6$

which is still true.

Point of order 2

The point $P = (x, y)$ is of order $2$ if and only if $P = -P$. Thus:

$(x, y) = (x, -y - a_1 x - a_3)$

$y = -y - a_1 x - a_3$

$2 y + a_1 x + a_3 = 0$

To view this from another perspective, let’s say the point $P = (x, y)$ is a point of order $2$. We know that the tangent at $P$ is vertical. Now, let’s fix $x$ and observe $F$ as a function of $y$ at $x$. We again consider $F$ with our head rotated by 90 degrees. The derivative of the observed function is $2y + a_1 x + a_3.$ We need

$2y + a_1 x + a_3 = 0$

to have a local extremum, which is where the point with the vertical tangent is.